Cordic Xoay Góc Thích Nghi là một thuật toán hiệu quả và linh hoạt được sử dụng rộng rãi trong các hệ thống nhúng và ứng dụng xử lý tín hiệu số. Thuật toán này cho phép tính toán các hàm lượng giác như sin, cos, tan, arctan và các phép toán xoay, chuyển đổi tọa độ một cách hiệu quả với phần cứng đơn giản, chỉ sử dụng phép cộng, phép trừ và phép dịch bit.
Cordic là gì?
Cordic là viết tắt của COordinate Rotation DIgital Computer, tức là máy tính số xoay tọa độ. Nó là một thuật toán lặp, sử dụng các phép xoay vi mô được xác định trước để đạt được góc xoay mong muốn. Mỗi phép xoay vi mô này tương ứng với một góc có tang là lũy thừa của 2 (arctan(2^-i)), giúp đơn giản hóa việc tính toán trên phần cứng.
Xoay Góc Thích Nghi với Cordic
Cordic xoay góc thích nghi là một phiên bản cải tiến của thuật toán Cordic truyền thống. Nó cho phép điều chỉnh động các tham số của thuật toán để tối ưu hóa hiệu suất và độ chính xác cho từng ứng dụng cụ thể. Việc thích nghi này có thể bao gồm thay đổi số lần lặp, lựa chọn các góc xoay vi mô khác nhau, hoặc sử dụng các kỹ thuật bù lỗi để giảm thiểu sai số tích lũy.
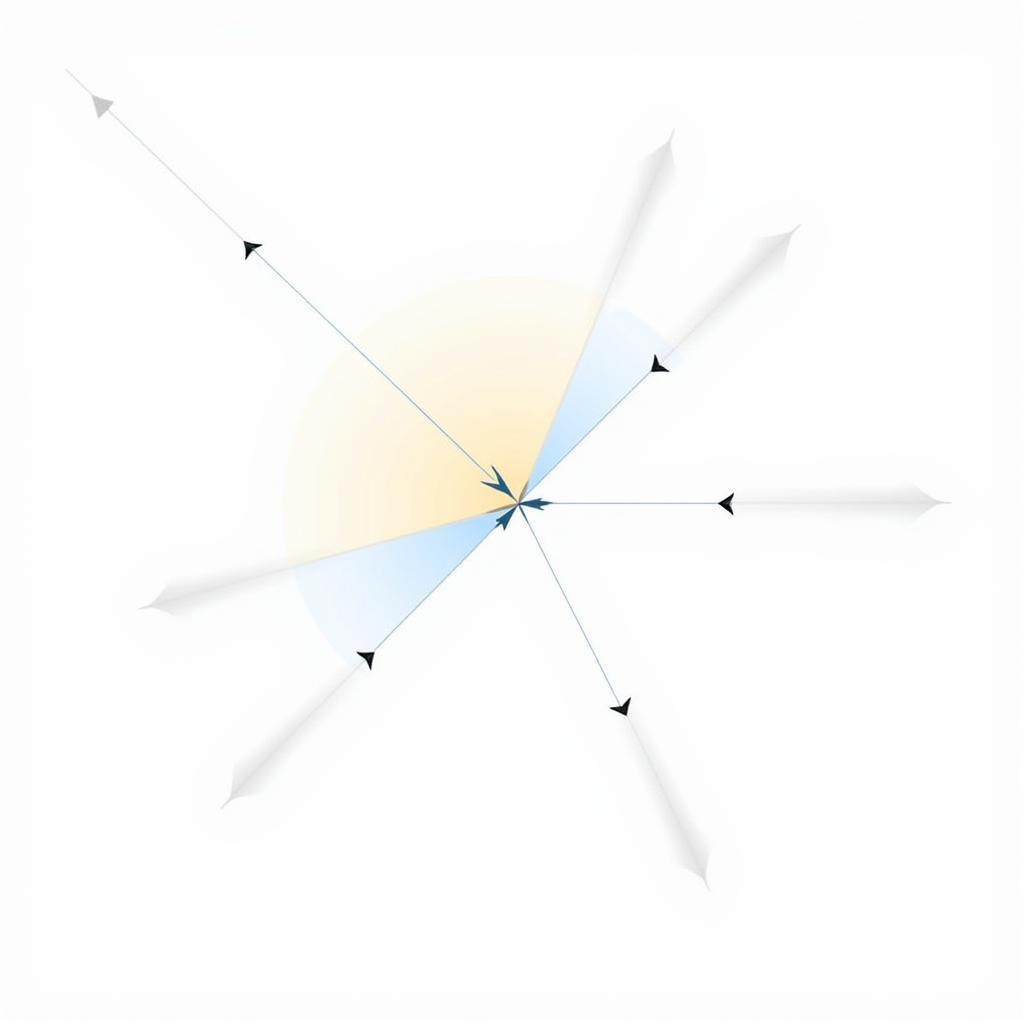 Minh họa xoay góc thích nghi với Cordic
Minh họa xoay góc thích nghi với Cordic
Ưu Điểm của Cordic Xoay Góc Thích Nghi
- Hiệu quả về phần cứng: Chỉ yêu cầu các phép cộng, phép trừ và phép dịch bit, giúp dễ dàng triển khai trên phần cứng với diện tích nhỏ và tiêu thụ năng lượng thấp.
- Linh hoạt: Có thể được điều chỉnh để đáp ứng các yêu cầu về độ chính xác và tốc độ khác nhau.
- Ứng dụng rộng rãi: Được sử dụng trong nhiều ứng dụng, từ xử lý tín hiệu số đến đồ họa máy tính và điều khiển robot.
Các Ứng Dụng của Cordic Xoay Góc Thích Nghi
Cordic xoay góc thích nghi được ứng dụng trong nhiều lĩnh vực khác nhau, bao gồm:
- Xử lý tín hiệu số: Tính toán FFT, lọc số, điều chế và giải điều chế.
- Đồ họa máy tính: Xoay và biến đổi hình ảnh, render 3D.
- Điều khiển robot: Điều khiển chuyển động của robot, tính toán quỹ đạo.
- Hệ thống định vị: Xác định vị trí và hướng.
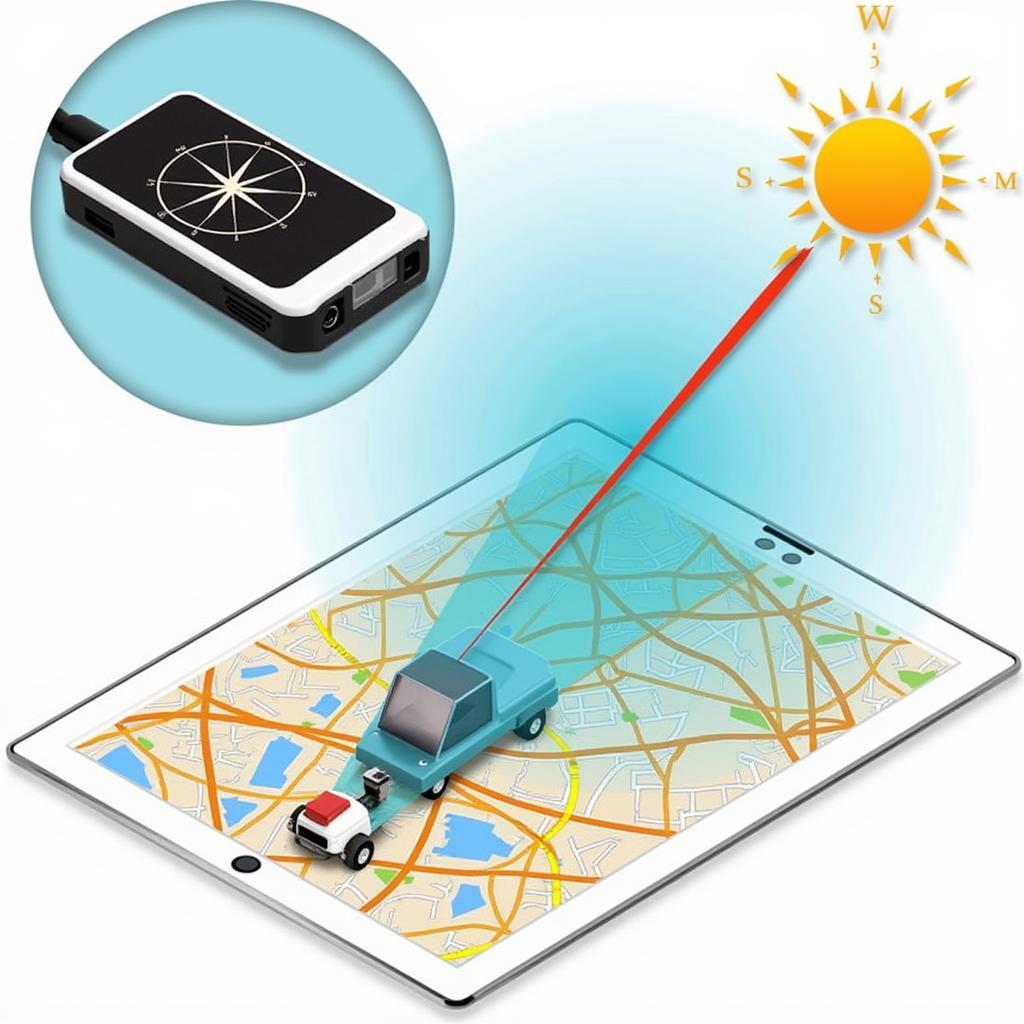 Ứng dụng của Cordic xoay góc thích nghi trong hệ thống định vị
Ứng dụng của Cordic xoay góc thích nghi trong hệ thống định vị
So Sánh Cordic với các Phương Pháp Khác
So với các phương pháp tính toán hàm lượng giác khác như sử dụng bảng tra cứu hoặc khai triển Taylor, Cordic xoay góc thích nghi có ưu điểm là hiệu quả về phần cứng và linh hoạt hơn. Bảng tra cứu yêu cầu bộ nhớ lớn, trong khi khai triển Taylor đòi hỏi nhiều phép nhân và chia, phức tạp hơn so với Cordic.
Lời khuyên từ chuyên gia
Theo Tiến sĩ Nguyễn Văn A, chuyên gia hàng đầu về xử lý tín hiệu số: “Cordic xoay góc thích nghi là một công cụ mạnh mẽ cho các hệ thống nhúng, đặc biệt là khi tài nguyên phần cứng bị hạn chế.”
Kết luận
Cordic xoay góc thích nghi là một thuật toán hiệu quả và linh hoạt cho phép tính toán các hàm lượng giác và phép xoay một cách hiệu quả trên phần cứng. Với khả năng thích nghi, Cordic đáp ứng được yêu cầu của nhiều ứng dụng khác nhau, từ xử lý tín hiệu số đến điều khiển robot. Việc hiểu rõ nguyên lý hoạt động và ứng dụng của Cordic xoay góc thích nghi sẽ giúp các kỹ sư thiết kế hệ thống nhúng tối ưu hơn về hiệu suất và tiêu thụ năng lượng.
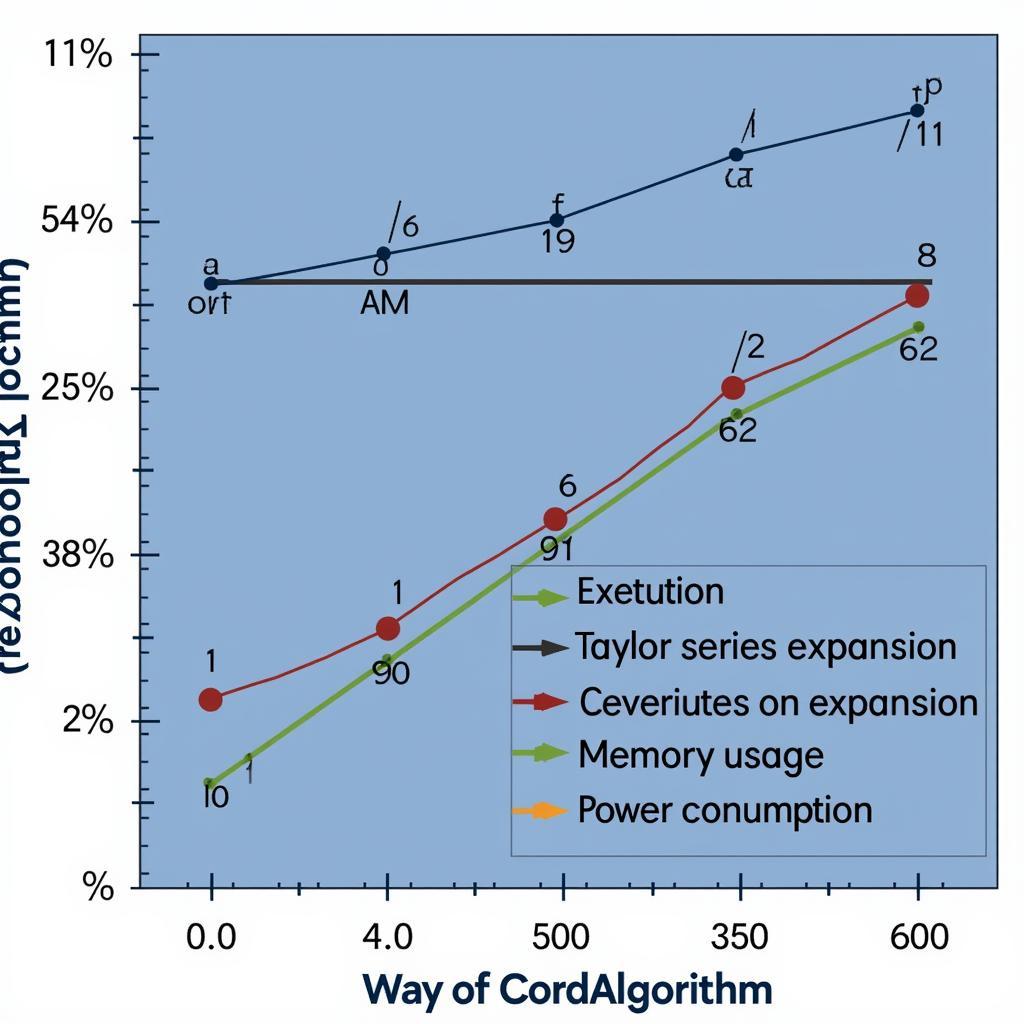 Biểu đồ so sánh hiệu suất của Cordic xoay góc thích nghi với các phương pháp khác
Biểu đồ so sánh hiệu suất của Cordic xoay góc thích nghi với các phương pháp khác
FAQ
- Cordic là gì? Cordic là viết tắt của COordinate Rotation DIgital Computer.
- Ưu điểm của Cordic là gì? Hiệu quả về phần cứng, linh hoạt và ứng dụng rộng rãi.
- Cordic được ứng dụng ở đâu? Xử lý tín hiệu số, đồ họa máy tính, điều khiển robot, hệ thống định vị.
- Tại sao Cordic thích nghi hiệu quả hơn Cordic truyền thống? Vì nó cho phép điều chỉnh động các tham số để tối ưu hóa hiệu suất.
- Cordic có phức tạp để triển khai không? Không, Cordic chỉ yêu cầu các phép cộng, phép trừ và phép dịch bit.
- Cordic có chính xác không? Độ chính xác của Cordic có thể được điều chỉnh bằng cách thay đổi số lần lặp.
- Có tài liệu nào để tìm hiểu thêm về Cordic không? Có rất nhiều tài liệu trực tuyến và sách về Cordic.
Mô tả các tình huống thường gặp câu hỏi.
Người dùng thường thắc mắc về việc triển khai Cordic trên phần cứng FPGA hoặc microcontroller, cách tối ưu hóa số lần lặp để đạt độ chính xác mong muốn, và so sánh hiệu năng giữa Cordic với các phương pháp tính toán hàm lượng giác khác.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về các thuật toán xử lý tín hiệu số khác, ví dụ như FFT, DFT, hoặc các bài viết về tối ưu hóa phần cứng cho hệ thống nhúng.