Bayes Giải Thích là một khái niệm thống kê quan trọng được sử dụng để cập nhật xác suất của một sự kiện dựa trên thông tin mới. Định lý này, được đặt theo tên của nhà toán học người Anh Thomas Bayes, đóng vai trò then chốt trong nhiều lĩnh vực, từ học máy và trí tuệ nhân tạo đến y học và tài chính.
Định Lý Bayes Là Gì?
Định lý Bayes cung cấp một công thức toán học để tính xác suất có điều kiện, nghĩa là xác suất của một sự kiện xảy ra dựa trên việc một sự kiện khác đã xảy ra. Nói cách khác, nó cho phép chúng ta cập nhật niềm tin của mình về một giả thuyết dựa trên bằng chứng mới.
Công Thức Bayes Giải Thích
Công thức Bayes có dạng như sau:
P(A|B) = [P(B|A) * P(A)] / P(B)Trong đó:
- P(A|B): Xác suất của sự kiện A xảy ra khi biết rằng sự kiện B đã xảy ra (xác suất hậu nghiệm).
- P(B|A): Xác suất của sự kiện B xảy ra khi biết rằng sự kiện A đã xảy ra (độ tin cậy).
- P(A): Xác suất tiên nghiệm của sự kiện A (niềm tin ban đầu về sự kiện A).
- P(B): Xác suất tiên nghiệm của sự kiện B (niềm tin ban đầu về sự kiện B).
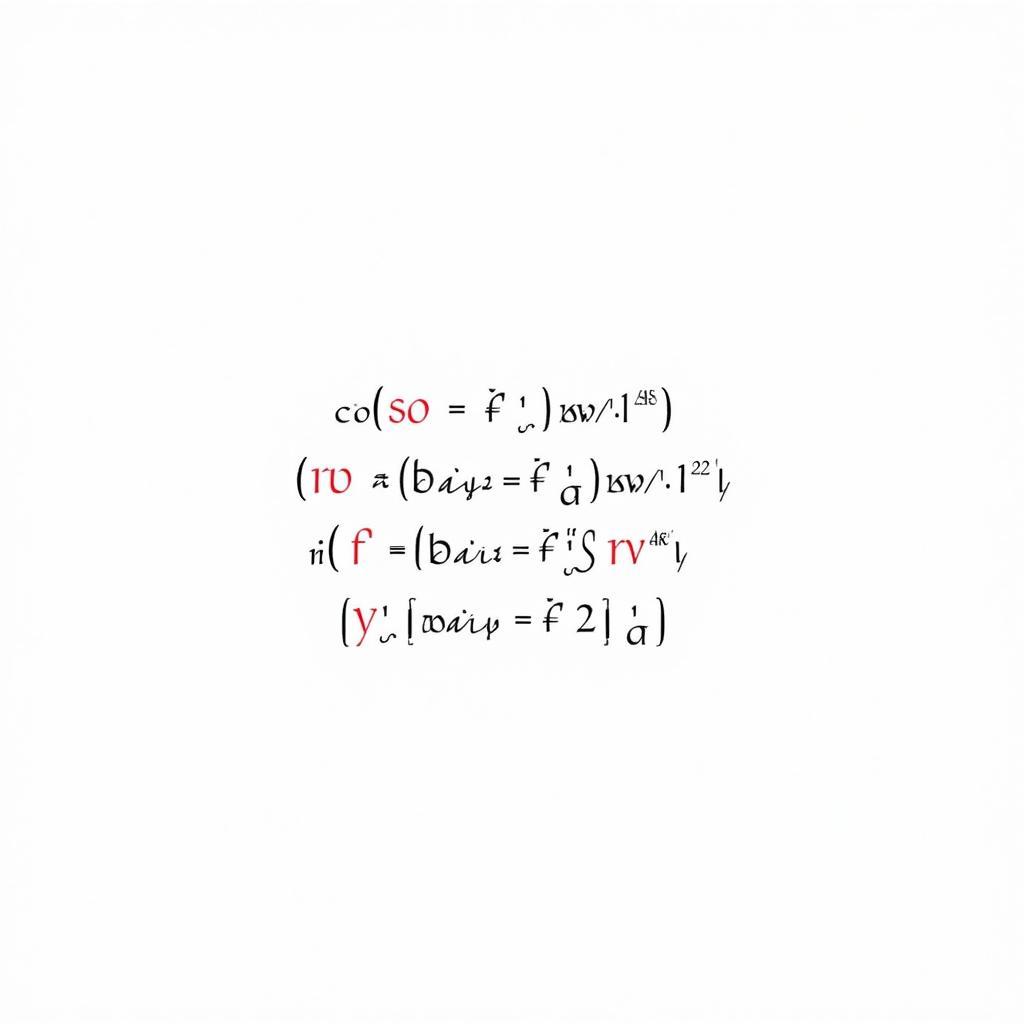Công Thức Bayes
Ví Dụ Bayes Giải Thích Trong Thực Tế
Để hiểu rõ hơn về cách thức hoạt động của Bayes giải thích, hãy xem xét một ví dụ đơn giản:
Giả sử chúng ta muốn xác định khả năng một người nào đó mắc bệnh X dựa trên kết quả xét nghiệm y tế. Biết rằng:
- Xác suất một người mắc bệnh X là 1% (P(A) = 0.01).
- Độ chính xác của xét nghiệm là 90%, nghĩa là nếu một người mắc bệnh X, xét nghiệm sẽ cho kết quả dương tính với xác suất 90% (P(B|A) = 0.9).
- Xác suất xét nghiệm cho kết quả dương tính ở những người không mắc bệnh X là 5% (tỷ lệ dương tính giả, P(B|¬A) = 0.05).
Bây giờ, giả sử một người có kết quả xét nghiệm dương tính. Vậy xác suất người này thực sự mắc bệnh X là bao nhiêu?
Áp dụng công thức Bayes, ta có:
- P(A|B) = Xác suất mắc bệnh X khi biết kết quả xét nghiệm dương tính.
- P(B|A) = 0.9
- P(A) = 0.01
- P(B) = P(B|A) P(A) + P(B|¬A) P(¬A) = (0.9 0.01) + (0.05 0.99) = 0.0585
Thay vào công thức, ta có:
P(A|B) = (0.9 * 0.01) / 0.0585 = 0.154
Do đó, xác suất người này thực sự mắc bệnh X khi biết kết quả xét nghiệm dương tính chỉ là khoảng 15.4%.
Ứng Dụng Bayes Trong Y Tế
Ứng Dụng Của Bayes Giải Thích
Định lý Bayes có nhiều ứng dụng rộng rãi trong các lĩnh vực khác nhau, bao gồm:
- Học máy: Phân loại văn bản, lọc thư rác, nhận dạng giọng nói.
- Trí tuệ nhân tạo: Hệ thống đề xuất, robot tự động.
- Y học: Chẩn đoán bệnh, phân tích dữ liệu y tế.
- Tài chính: Dự đoán thị trường, quản lý rủi ro.
- Khoa học máy tính: Xử lý ngôn ngữ tự nhiên, thị giác máy tính.
Kết Luận
Bayes giải thích cung cấp một công cụ mạnh mẽ để cập nhật niềm tin của chúng ta dựa trên bằng chứng mới. Từ việc chẩn đoán bệnh đến phân loại email spam, định lý Bayes đã và đang đóng vai trò quan trọng trong việc giải quyết các vấn đề phức tạp trong thế giới thực.
FAQs
1. Định lý Bayes có thể được sử dụng cho các sự kiện độc lập không?
Không, định lý Bayes chỉ áp dụng cho các sự kiện có điều kiện, tức là các sự kiện có liên quan đến nhau.
2. Xác suất tiên nghiệm có ảnh hưởng đến kết quả của Bayes giải thích không?
Có, xác suất tiên nghiệm đóng vai trò quan trọng trong việc xác định xác suất hậu nghiệm.
3. Làm thế nào để xác định độ tin cậy (P(B|A)) trong thực tế?
Độ tin cậy thường được xác định thông qua các thí nghiệm, nghiên cứu hoặc dữ liệu lịch sử.
4. Có những hạn chế nào khi sử dụng Bayes giải thích?
Một hạn chế của Bayes giải thích là việc xác định xác suất tiên nghiệm chính xác có thể khó khăn trong một số trường hợp.
5. Tôi có thể tìm hiểu thêm về Bayes giải thích ở đâu?
Bạn có thể tìm thấy nhiều tài liệu trực tuyến về Bayes giải thích, bao gồm các bài báo khoa học, sách giáo khoa và video hướng dẫn.
Bạn muốn tìm hiểu thêm về các chủ đề liên quan?
Bạn cần hỗ trợ?
Liên hệ với chúng tôi:
- Số điện thoại: 0915063086
- Email: [email protected]
- Địa chỉ: LK 364 DV 08, Khu đô thị Mậu Lương, Hà Đông, Hà Nội 12121, Việt Nam.
Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.